本文共 3804 字,大约阅读时间需要 12 分钟。
十二年前,为了解决支付宝第一代架构在迅猛发展的业务面前捉襟见肘的困境,蚂蚁金服技术团队开启了一次前所未有的尝试。创新都是被逼出来的,今天高速发展的SOFAStack同样如此。
十二年时间,几代蚂蚁技术人参与攻坚,SOFA走出了一条跟传统金融行业不同的分布式架构之路。这条路,既要基于不可靠的硬件系统实现金融级的性能和可靠性,又要应对支付宝这样的超大规模互联网金融应用,很不容易,但蚂蚁技术团队做到了。今天,就让我们聊聊SOFAStack的前世今生。
SOFA缘起
2006年,支付宝面临的最大问题是业务变得越发复杂,工程师数量也越来越多,原来的单体系统逐渐无法装载更多更复杂的业务逻辑,也不能让大量工程师一起并行工作。当时的支付宝希望,系统可以做到成百上千个项目并行进行,并且每个工程师可以不受干扰地工作,当业务逻辑增加的时候,系统的复杂度不至于指数级上升。技术团队要做对未来的技术架构做一个选择。
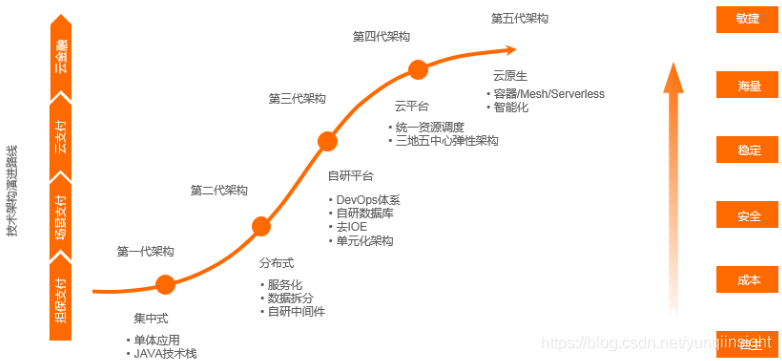
支付宝团队做了一个决定,要走一条过去没有人走过的路,启动了支付宝技术系统的服务化之路,也是支付宝第二代架构的由来。2007年开始,支付宝启动了对交易系统、商户系统、会员系统、支付清算系统的改造。
当时担任支付宝首席架构师的程立,给要做的这套分布式架构起了一个“SOFA”的名字,其背后有两个含义:一是按照当时的技术趋势,要做面向服务的架构,即Service Oriented Architecture,但加入了金融业务,所以是Service Oriented Fabric Architecture;二是希望能够像沙发一样,让工程师可以非常爽地工作。
第一代的SOFA其实就解决两个问题:一是当要把系统变成分布式的时候,怎么有一个像“胶水”一样的连接器机制,可以把分布式系统连接成一个整体;二是希望每一个服务本身是组件化的,所以当时第一代SOFA里采用了OSGi(一套Java模块化规范,允许应用程序使用精炼、可重用和可协作的组件构建),这样每个工程师可以专注于各自的组件,最后又能够把这些组件拼装在一起成为“服务”,再把“服务”拼装在一起成为整个大系统。这一整套框架,就是第一代SOFA框架。
2008年1月,SOFA项目上线,成为蚂蚁金服延用12年之久并持续打磨至今且对外开源的一套技术架构。
SOFA技术演进
SOFA的版本迭代跟蚂蚁金服的架构发展是密切相关的,作为一个演进了十多年的框架,它也一定程度上代表了蚂蚁金服的技术体系演变。
从第一代到眼下的第五代,SOFA的演进过程其实是支付宝从最早的大型业务与IT交织在一起的单体系统,一边拆金融业务系统(即后来的业务中台)、一边拆底层IT系统(即后来的数据中台、计算中台)的过程,在拆分的过程中还要解决新出现的可扩展性、一致性问题等各种问题,同时不断应付每年都能击穿系统极限的双十一,还要把数据从原有系统一点一点“倒腾”到新系统里、同时管理新增的海量数据。
蚂蚁金服金融产品技术部总经理杨冰透露,“SOFA中间件在蚂蚁内部经历了十年的发展和五代架构的演进,被广泛应用在包括支付、借贷、信用、基金、保险等全金融场景,支撑着蚂蚁平稳度过历次双十一、双十二、新春红包等大考,创造了25.6万笔每秒的交易纪录,并还在不断刷新这个纪录。”
早期的SOFA在项目推进的过程中既有研发平台又有研发上层的业务系统,相当于把很多风险都导在一个项目里面一起做,SOFA第一代项目就是靠团队齐心协力,每天都会遇到新问题、每天都要去解决各种问题,但大家背后有必胜信念而且非常拥抱变化,敢于在项目的中后期把前期架构决定全部推翻掉,再用一套新的架构替代
杨冰提到,随着每年的交易量的不断上升,逼着技术团队必须从单体架构转到服务化架构,然后演进到单元化架构、弹性架构。SOFA 大部分的功能升级都是伴随着整个公司的技术架构目标上的更大挑战进行的。
杨冰完整经历了SOFA1到SOFA2的开发过程,从SOFA1整体完成落地,到SOFA2引入了服务的架构。到了SOFA3蚂蚁团队把Tomcat JBoss层替换为自研的应用服务器,解决了内部系统做类隔离、模块隔离以及合并部署的问题。
而现在,SOFA已经逐渐从解决分布式服务和分布式交易的问题,变成一个真正解决金融级系统构建的基础架构问题。这也是SOFA改名的原因,从原来的Service Oriented Fabric Architecture改为Scalable Open Financial Architecture:
- Scalable代表着这个框架可以真正解决金融级系统的异地多活的容灾和扩展问题,而且SOFA的可扩展能力不仅是处理更多的交易,还可容纳更多的业务,能够让几千位工程师甚至未来上万个工程师一起协同工作;
- Open的意思是希望这个框架可以让业务应用非常容易使用,又能与经典架构系统有机融合,SOFA框架未来不但可以编排蚂蚁金服工程师自己写的业务逻辑,而且可以编排合作伙伴的业务逻辑,成为一个完整的编排框架;
- Financial则意味着SOFA必须是具备金融级属性,能真正实现金融级的一致性、可用性和稳定性。
走向开源
开发者看开源,看到的可能是情怀。商业公司看开源,看到的可能是共赢。
对于蚂蚁金服来说,开源可以扩大技术服务场景,为支付、金融等更多的客户提供服务,提升合作伙伴的效率。虽然,蚂蚁金服已经有很多的业务场景,也在很多场景下取得了超大规模的实践经验,但是,依然存在没有覆盖到的金融服务场景。
因此,选择将技术开源出来,可以供更多的客户应用到其自身的场景下,这些场景有效地补充了蚂蚁金服的技术应用面,也为更完善的技术框架奠定了基础。所以,蚂蚁选择将SOFA中间件框架逐步开源,在贡献给社区的同时,也期望社区、合作伙伴、客户一起参与共建,形成行业标准和最佳实践。
对金融服务而言,监管和自主可控的要求更多,开源是一种可以使客户和上下游产业共同参与和发展的可行模式。SOFA走向开源并不是技术部门去说服公司决策层开源,而是业务发展的自然选择,也是一种合理的发展方向。
开源并不是简单地将代码上传到GitHub上,前期面临很多繁重的工作,也正因如此,SOFA直到发展到第四代才做好了开源的准备。
杨冰表示,从 SOFA3 到 SOFA4 的发展过程当中,轻量化的动作其实就是在为开源做准备,一些公用能力都希望能开源出来。蚂蚁技术团队开源SOFA不会把它的代码分为完全两套东西,然后两个分别演进,这不是开源的正确做法。除此以外,开源对整个团队的消耗非常大,蚂蚁也希望用同一套代码来实现内部的兼容和外部的开源,在开源的代码中留一些比较好的扩展点,这对SOFA本身代码架构的可扩展性也是一大挑战。
“但这是值得的,在为开源代码做改进时,也是为公司自己的业务做改进,这是双赢且可持续发展的。”杨冰补充道。
拥抱Service Mesh
Service Mesh是近两年来比较火的技术概念,进入SOFA 5时代,SOFA也全面拥抱了金融级云原生,其中Service Mesh已经在内部大规模落地,并接受双十一实战检验。
蚂蚁金服在中间件方面的探索比较深远,规模也相当大。在杨冰看来,随着基础技术平台逐步走向云化,ServiceMesh将会是连接现在这个时代和云原生时代的桥梁,也是把基础设施沉淀到蚂蚁金服整个技术平台当中非常关键的一环。随着容器技术的兴起,可以将以往的中间件组建拆分得更细、更灵动,并且资源利用率和运维效率也将得到进一步的改善。

蚂蚁金融级云原生架构已在内部大规模落地,Service Mesh是金融级云原生的重要基础设施之一。在2019年双十一大促中,Service Mesh架构已经100%覆盖蚂蚁金服核心支付链路,几十万容器,峰值千万QPS,平均RT 0.2ms,是业界最大的 Service Mesh 集群,成为金融级云原生基础设施。通过Service Mesh架构的资源分时复用技术,大规模统一资源调度,在同时支撑天猫双11和经济体用户增长两个大促的同时,实现了零IT成本增加。SOFAStack 双模微服务平台也在近日正式发布,提供了既支持 SOFA 框架又支持 Service Mesh 架构的微服务管理和治理能力。
SOFAStack,走向未来
回顾SOFAStack十多年来走过的那些艰辛困苦、高光时刻,背后默默耕耘的既有蚂蚁金服技术团队最初的架构师们、CTO们,也有一代代的基层工程师们。今天的SOFAStack,已经站在了技术的最前沿,用最先进的技术解决金融行业最艰难的问题,但故事,还在继续。
未来的SOFA将持续拥抱开源,与社区、合作伙伴、客户一起共建,并将经过内部实践的开源改进回馈给开源社区。目前SOFA已经在网商银行、中国人保健康、南京银行等金融机构中落地,未来也将持续输出给外部合作伙伴。SOFA已于9月份上线阿里云,通过全面整合金融科技与服务能力,持续为金融行业提供技术底座支撑。

未来,SOFA还继续探索和实践金融级云原生,拥抱ServiceMesh、Serverless,以开源共建的方式促进云原生技术的落地与迭代,并将蚂蚁的技术经验赋能给金融业界,真正让SOFA这一金融级分布式架构,能够帮助到万千的金融领域技术从业者们。
本文为云栖社区原创内容,未经允许不得转载。